CS61B 笔记

这篇笔记包括了 CS61B 排序之前的部分的笔记，不包括项目和 lab

为什么不包括排序部分呢，主要是因为之前学习过相关的内容，在看 61B 的时候便省略掉了，至于项目部分，我会将 gitlet 单独写为一篇笔记发布

By：思源南路世一劈

Week 1

6 月 29 日

CS61B，启动！

虽然之前在学校简单把 Week 1 的内容看完了并且把 proj0 写完了，但是现在已经基本忘记了，所以现在开始重新开始我的数据结构学习之旅！

Java 简介

Java 是面向对象编程的语言，在 CS61B 中将担任我们主要使用的语言

Hello world

1
2
3
4
5
public class HelloWorld {
    public static void main(String[] args) {
        System.out.println("Hello world!");
    }
}

以上为 Java 中 Hello world 程序的代码，由该代码块我们可以理解 Java 程序的基本结构：

  • Java 程序文件均由一个个类构成，体现其面向对象编程的特点
  • 类名与文件名相同
  • main 函数为类的主函数，其中String args[]表示 main 函数的参数(记住就行)
  • System.out.println()是 Java 的输出函数，类比 C++中的cout和printf

运行 Java 程序

执行 Java 程序最常见的方法是通过两个程序的序列运行它。第一个是 Java 编译器，或 javac 。第二个是 Java 解释器，或 java

compilationflow

例如，要运行 HelloWorld.java ，我们会在终端中输入命令 javac HelloWorld.java ，然后输入命令 java HelloWorld 。结果会类似于这样：

1
2
3
$ javac HelloWorld.java
$ java HelloWorld
Hello World!

其他基本语法

循环，条件等语法同 C++相同，不再赘述，即for循环，while循环和，if-else条件语句

Java 中类和函数

Java 中的函数

由于所有的 Java 代码都是类的一部分，我们必须定义函数，使其属于某个类。属于类的函数通常被称为“方法”。

  • 返回类型可类比 C++：void,int,double等
  • public前缀表示这个函数是该类的公共方法，相对应的是 private

一个基础 Demo 如下，效果为返回较大的数：

1
2
3
4
5
6
7
8
9
10
11
12
public class LargerDemo {
    public static int larger(int x, int y) {
        if (x > y) {
            return x;
        }
        return y;
    }

    public static void main(String[] args) {
        System.out.println(larger(8, 10));
    }
}

Java 中的类

总体来说，Java 中类的基本语法同 C++中大体相似，例如使用 . 来调用类的函数以及变量，又例如this指针等，这里列出比较重要的几点：

  • new关键字：用来实例化类变量，注意，虽然 Java 中没有严格意义上的指针，但new的逻辑事实上也可以类比 C++中的类的指针申请新的动态变量，例如如下代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public class Dog {
    public int weightInPounds;

    public Dog(int w) {
        weightInPounds = w;
    }

    public void main(String[] args) {
        Dog A = new Dog(20);
        Dog B;
        B = A;
        B.weightpounds = 30;
    }
}

这段代码执行后，A 与 B 事实上是同一条狗，它们的体重都是 30

  • static关键字：

Java 允许我们定义两种类型的方法：

  1. 类方法，又称静态方法
  2. 实例方法，又称非静态方法

实例方法是只能由类的特定实例执行的操作。静态方法是由类本身执行的操作。在不同情况下，两者都很有用。作为静态方法的一个示例， Math 类提供了一个 sqrt 方法。因为它是静态的，我们可以按照以下方式调用它：

1
x = Math.sqrt(100);

如果 sqrt 是一个实例方法，我们将会有下面这种尴尬的语法。幸运的是 sqrt 是一个静态方法，所以我们在真实的程序中不必这样做

1
2
Math m = new Math();
x = m.sqrt(100);

有时候，拥有一个同时包含实例方法和静态方法的类是有意义的。例如，假设想要比较两只狗的能力。做到这一点的一种方法是添加一个用于比较狗的静态方法

1
2
3
4
5
6
public static Dog maxDog(Dog d1, Dog d2) {
    if (d1.weightInPounds > d2.weightInPounds) {
        return d1;
    }
    return d2;
}

这种方法可以被调用，例如：

1
2
3
Dog d = new Dog(15);
Dog d2 = new Dog(100);
Dog.maxDog(d, d2);

观察到我们已经使用类名调用，因为这个方法是一个静态方法

同理，使用static关键字定义的变量即为静态变量，可由类名直接调用

Week 2

7 月 1 日

JUnits

写的代码是需要测试的，从头开始，我们可以写自己的测试程序：

假设我们有一个给字符串数组排序的类 Sort，我们现在需要给它编写测试：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class TestSort {
    /** Tests the sort method of the Sort class. */
    public static void testSort() {
        String[] input = {"i", "have", "an", "egg"};
        String[] expected = {"an", "egg", "have", "i"};
        Sort.sort(input);
        for (int i = 0; i < input.length; i += 1) {
            if (!input[i].equals(expected[i])) {
                System.out.println("Mismatch in position " + i + ", expected: " + expected + ", but got: " + input[i] + ".");
                break;
            }
        }
    }

    public static void main(String[] args) {
        testSort();
    }
}

很显然，这是最原始的方法，吃力不讨好

org.junit 库提供了许多有用的方法和功能，可以简化测试编写。例如，我们可以用以下方法替换上面的简单的临时测试：

1
2
3
4
5
6
public static void testSort() {
    String[] input = {"i", "have", "an", "egg"};
    String[] expected = {"an", "egg", "have", "i"};
    Sort.sort(input);
    org.junit.Assert.assertArrayEquals(expected, input);
}

进一步简化，可以得到更舒适的写代码体验：

我们将讨论两个主要的增强功能

第一个增强是使用所谓的“测试注释”。为此，我们：

  • 在每个方法之前加上 @org.junit.Test （不要分号）。
  • 将每个测试方法更改为非静态。
  • 从 TestSort 类中删除我们的 main 方法。

一旦我们完成了这三件事，如果我们在 JUnit 中使用 Run->Run 命令重新运行我们的代码，所有的测试都会执行，而无需手动调用。这种基于注解的方法有几个优点：

  • 无需手动调用测试。
  • 所有测试都会运行，不仅仅是我们指定的那些。
  • 如果一个测试失败，其他测试仍然会继续运行。
  • 提供了运行了多少次测试以及有多少次测试通过的计数。
  • 测试失败时的错误消息看起来好多了。
  • 如果所有测试都通过，我们会收到一条好消息，并且会出现一个绿色的条形图，而不是什么输出都没有。

第二个增强功能将允许我们对一些非常冗长的方法名称以及注解名称使用更短的名称。具体来说，我们将使用所谓的“导入语句”。

我们首先在文件顶部添加导入语句 import org.junit.Test; 。这样做之后，我们可以将所有 @org.junit.Test 的实例替换为简单的 @Test 。

然后我们添加第二个导入语句 import static org.junit.Assert.* 。这样做之后，我们可以在任何地方省略我们之前有 org.junit.Assert. 的地方。例如，我们可以用简单地 assertEquals(expected2, actual2); 替换 org.junit.Assert.assertEquals(expected2, actual2);

1
2
3
4
5
6
7
@Test
public static void testSort() {
    String[] input = {"i", "have", "an", "egg"};
    String[] expected = {"an", "egg", "have", "i"};
    Sort.sort(input);
    assertArrayEquals(expected, input);
}

如上所示

Lists

从 0 开始创建自己的列表！

IntLists

初始设想是利用链表：

1
2
3
4
5
6
7
8
9
public class IntList {
    public int first;
    public IntList rest;

    public IntList(int f, IntList r) {
        first = f;
        rest = r;
    }
}

SLList

显然，在这上面直接添加函数方法会很裸奔，我们选择将核心提出，并创建新的类：

1
2
3
4
5
6
7
8
9
public class IntNode {
    public int item;
    public IntNode next;

    public IntNode(int i, IntNode n) {
        item = i;
        next = n;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
public class SLList {
    public IntNode first;

    public SLList(int x) {
        first = new IntNode(x, null);
    }

    /** Adds an item to the front of the list. */
    public void addFirst(int x) {
        first = new IntNode(x, first);
    }
}

这里的 SLList 即为新的列表数据结构，同样的，可以添加得到一系列实用的方法，如addfirst,addlast,getfirst,getlast,但是这时得到的数据结构仍然有不方便以及危险的地方：

  • first 结点依然裸奔!
  • 空列表无法舒适地 addlast

为此，我们继续优化，首先将结点类型改为 private，其次设置哨兵结点(sentinel)，即添加一个始终位于最前端的结点，确保数据结构不是空的，这样便以一种类似数分中“一致连续”的手法处理了上述问题，实现了一致性。这也是编写代码的重要原则之一

代码就略了，我懒

实际上不会改变 A 中数据的值，因为这里的 x 也是 A 中数据按照值传递到 x 的

Week 3

7 月 3 日

Lists

(续 Week 2 中的 SLLists 部分)

在 SLList 中，我们优化了裸数据结构带来的不便，同时添加了哨兵结点来维持不变性，但是，这样的 Lists 仍然具有一些可以优化的地方：

  • addLast时，总会遍历整个链表，如果我的列表长达一百万项，这将浪费时间
  • 单向遍历，不利于快速访问元素/删除元素，尤其是靠后的元素，每次访问都需要经历不必要的遍历

由此，我们引出双向链表——Double Linked List，即DLList

DLList

添加前向指针(这个说法不严谨但是我先这么写)，使得列表变成可以双向访问的类型：

1
2
3
4
5
public class IntNode {
    public IntNode prev;
    public int item;
    public IntNode next;
}

同时为末端结点同样设置一个哨兵结点，由此得到的数据结构会类似下面的拓扑图：

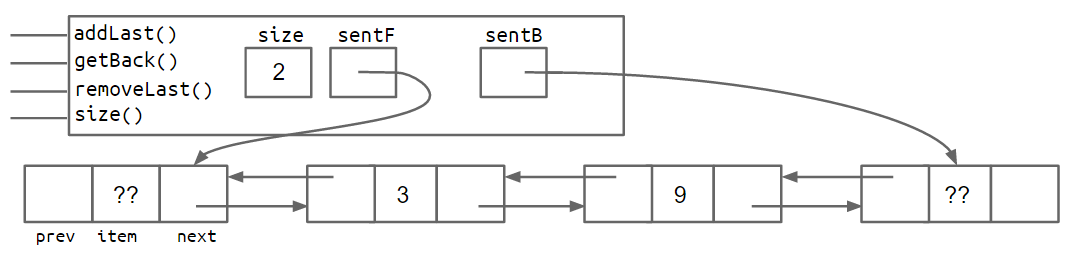
dllist_double_sentinel_size_2.png

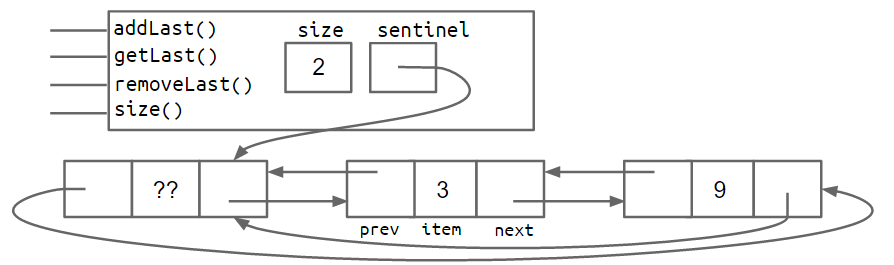
也可以首尾共用一个哨兵结点，实现环形结构：

dllist_circular_sentinel_size_2.png

最后，加入“模板”(在 C++里是模板)，使得我们的列表“通用化”——

一个可以容纳任何类型的通用 DLList 看起来如下：

1
2
3
4
5
6
7
8
9
10
11
12
public class DLList<BleepBlorp> {
    private IntNode sentinel;
    private int size;

    public class IntNode {
        public IntNode prev;
        public BleepBlorp item;
        public IntNode next;
        ...
    }
    ...
}

现在我们已经定义了一个 DLList 类的通用版本，我们还必须使用特殊的语法来实例化这个类。为此，在声明时，我们将所需的类型放在尖括号内，并在实例化时使用空的尖括号。例如：

1
2
DLList<String> d2 = new DLList<>("hello");
d2.addLast("world");

由于泛型仅适用于引用类型，我们无法将原始类型如 int 或 double 放入尖括号中，例如 <int> 。相反，我们使用原始类型的引用版本，在 int 情况下是 Integer ，例如。

1
2
DLList<Integer> d1 = new DLList<>(5);
d1.insertFront(10);

有关使用通用类型的更多细微差别，我们将把它们推迟到本书的后面章节。现在，请使用以下经验法则：

  • 在实现数据结构的.java 文件中，在类名之后的文件顶部只需指定一次泛型类型名称。
  • 在其他 .java 文件中，使用您的数据结构时，在声明时指定特定的期望类型，并在实例化时使用空的尖括号运算符。
  • 如果您需要实例化一个泛型到原始类型，请使用它们的原始等效项 Integer ， Double ， Character ， Boolean ， Long ， Short ， Byte 或 Float 。

细节：在实例化时，您也可以在尖括号内声明类型，尽管这并非必需，只要您也在同一行上声明变量。换句话说，下面的代码行是完全有效的，即使右侧的 Integer 是多余的。

1
DLList<Integer> d1 = new DLList<Integer>(5);

AList

最后，我们将使用另一种不同的手法来实现 List——数组！这样可以极大优化查找元素带来的时间损失，首先下面是数组相关的基础知识：

Array(数组)

实例化数组的三种方法：

  • x = new int[3];
  • y = new int[]{1, 2, 3, 4, 5};
  • int[] z = {9, 10, 11, 12, 13};

包含数组基本操作的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int[] z = null;
int[] x, y;

x = new int[]{1, 2, 3, 4, 5};
y = x;
x = new int[]{-1, 2, 5, 4, 99};
y = new int[3];
z = new int[0];
int xL = x.length;

String[] s = new String[6];
s[4] = "ketchup";
s[x[3] - x[1]] = "muffins";

int[] b = {9, 10, 11};
System.arraycopy(b, 0, x, 3, 2);

最后一行展示了一种将信息从一个数组复制到另一个数组的方法。 System.arraycopy 接受五个参数：

  • The array to use as a source
  • Where to start in the source array
  • The array to use as a destination
  • Where to start in the destination array
  • How many items to copy

System.arraycopy(b, 0,x, 3, 2) 相当于 Python 中的 x[3:5] = b[0:2]

AList(使用数组实现列表)

这一节有趣的主要是如何在数组满员时“扩展数组”，一开始我们使用的是逐 1 相加，但是测试结果表明这样的效率甚至远远不如 SLList !

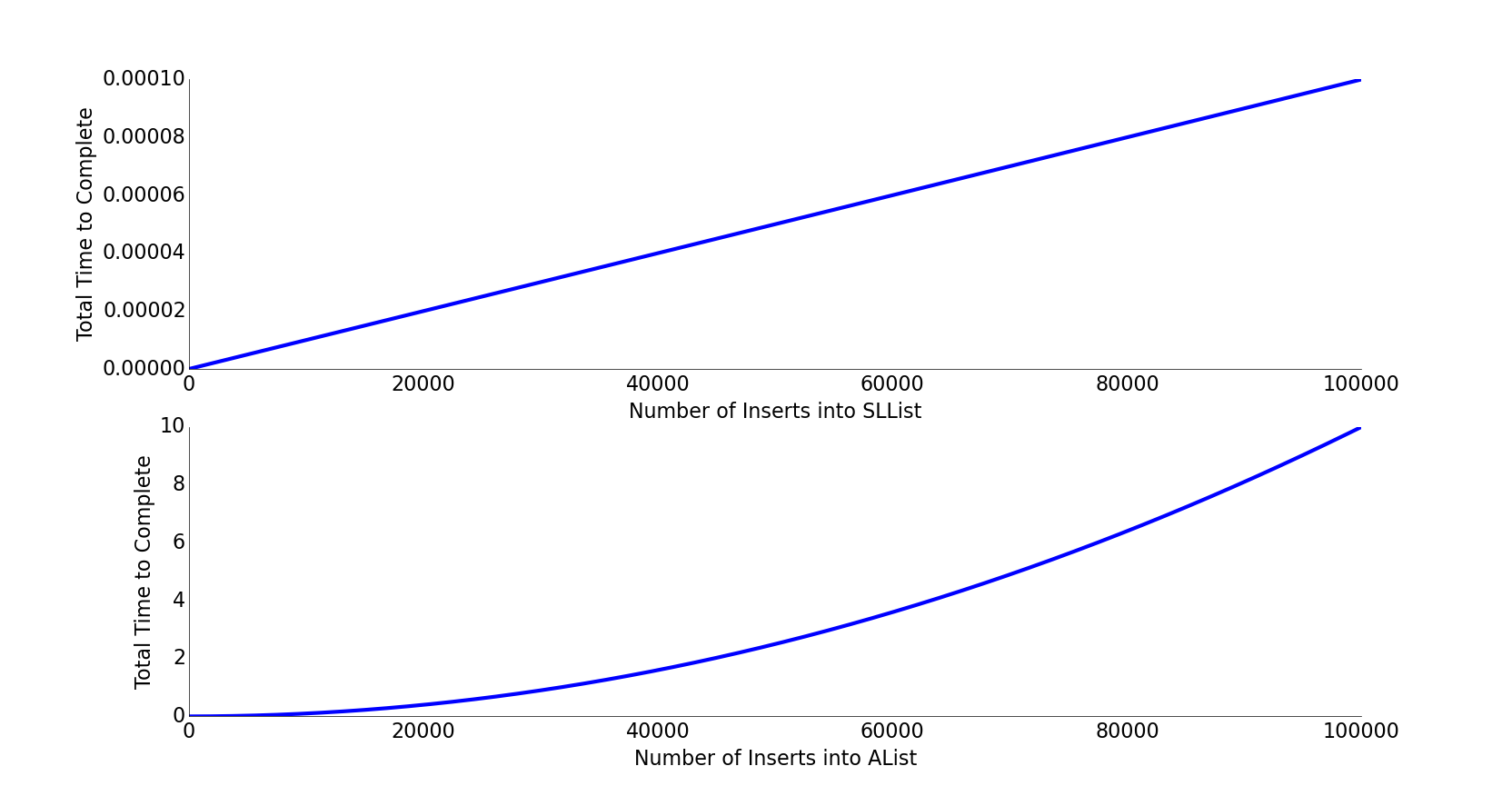fig25/insert_experiment.png将加的数额改成 100？1000？不，这样做的时间消耗始终是平方级别的，我们使用乘法来扩展数组，实现效率的极大提升！

1
2
3
4
5
6
7
public void insertBack(int x) {
    if (size == items.length) {
           resize(size + RFACTOR);
    }
    items[size] = x;
    size += 1;
}
1
2
3
4
5
6
7
public void insertBack(int x) {
    if (size == items.length) {
           resize(size * RFACTOR);
    }
    items[size] = x;
    size += 1;
}

最后记得将 AList 数组列表模板化，以适应不同的使用需求

注意这里的语法有细微区别，这是 Java 中数组的特性所决定的：

Java 不允许我们创建一个泛型对象数组，因为泛型的实现方式存在一个模糊的问题。也就是说，我们不能做类似以下的事情：

1
Glorp[] items = new Glorp[8];

相反，我们必须使用下面的抽象语法：

1
Glorp[] items = (Glorp []) new Object[8];

这将产生一个编译警告，暂时不用管。我们将在后面更详细地讨论

Inheritance and Implements

继承与实现！继续学习 Java 的编程特性，同时更加深入地学习列表等数据结构！这一节的内容主要包括：继承，转换，扩展，高阶函数，多态与 Java 库和包，我们书接上文，从我们熟悉的 SLList 和 DLList，AList 讲起······

假设我们有一个计算最长单词的函数：

1
2
3
4
5
6
7
8
9
10
11
public static String longest(SLList<String> list) {
    int maxDex = 0;
    for (int i = 0; i < list.size(); i += 1) {
        String longestString = list.get(maxDex);
        String thisString = list.get(i);
        if (thisString.length() > longestString.length()) {
            maxDex = i;
        }
    }
    return list.get(maxDex);
}

对于 AList 类型的列表怎么办？我们当然可以使用函数重载(Overload，类比 C++)，写两个一模一样的方法：

1
2
3
4
5
6
7
8
9
10
11
public static String longest(AList<String> list) {
    int maxDex = 0;
    for (int i = 0; i < list.size(); i += 1) {
        String longestString = list.get(maxDex);
        String thisString = list.get(i);
        if (thisString.length() > longestString.length()) {
            maxDex = i;
        }
    }
    return list.get(maxDex);
}

真是颇费笔墨！呃啊！代码维护性降低了！以后有新的列表类型加入时还得再写一遍！

类比 C++中子类与父类的操作，我们直接掏出Inheritance，御敌于国门之外——

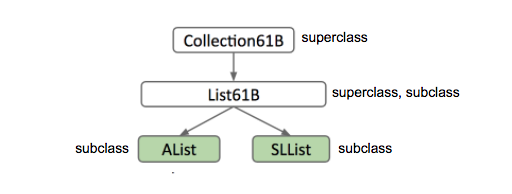
subclass

Interface Inheritance

接口继承

首先登场的是接口继承(虽然这个翻译怪怪的)！选用 List61B 作为二者的超类，注意这里的语法规则：

1
2
3
4
5
6
7
8
9
10
public interface List61B<Item> {
    public void addFirst(Item x);
    public void add Last(Item y);
    public Item getFirst();
    public Item getLast();
    public Item removeLast();
    public Item get(int i);
    public void insert(Item x, int position);
    public int size();
}

接下来，我们在两个子类中分别实现上述方法即可，注意声明类的时候的特殊语法！

1
public class AList<Item> implements List61B<Item>{...}

implements List61B<Item> 本质上是一个承诺。AList 表示“我承诺我将拥有并定义 List61B 接口中指定的所有属性和行为”，二者的关系实际上是**”is-a”，不是“has-a”**

Overriding

在子类中实现所需的功能时，在方法签名的顶部包含 @Override 标签是有用的（实际上在 61B 中是必需的）。在这里，我们只为一个方法做了这样的操作。

1
2
3
4
@Override
public void addFirst(Item x) {
    insert(x, 0);
}

即使不包括此标签，也可以覆盖该方法。因此，在技术上不必包括它。但是，包括标签可以作为程序员的保障，向编译器发出警告，表明您打算覆盖此方法。假设要覆盖 addLast 方法。如果您入错误并意外地写成 addLsat 会怎么样？如果不包括@Override 标签，那么可能无法发现错误。而如果您包括@Override，编译器将会停止并提示在程序运行之前修复错误。

Implement Inheritance

实现继承

我们也可以在超类中即对某些方法进行实现，对于不需要重写该方法的子类，调用该方法即直接调用超类的实现，而也有的子类需要重写该方法，再各做修改即可。为了做到这一点，必须在方法签名中包含 default 关键字。

1
2
3
4
5
6
default public void print() {
    for (int i = 0; i < size(); i += 1) {
        System.out.print(get(i) + " ");
    }
    System.out.println();
}

List61B 类的所有子类都可以使用这个方法！

然而，对于 SLList， get 方法需要在每次调用时遍历整个列表。最好在遍历时直接打印！我们希望 SLList 以不同于其接口规定的方式打印。为了做到这一点，我们需要覆盖它。在 SLList 中，我们实现了这个方法；

1
2
3
4
5
6
@Override
public void print() {
    for (Node p = sentinel.next; p != null; p = p.next) {
        System.out.print(p.item + " ");
    }
}

现在，每当我们在 SLList 上调用 print()时，它将调用这个方法，而不是 List61B 中的方法。

静态类型与动态类型

Java 怎么知道使用哪个方法？这就需要提到我们的静态类型与动态类型——

假设有以下代码(这是合法的)：

1
List61B<String> lst = new SLList<String>();

In the above declaration and instantiation, lst is of type “List61B”. This is called the “static type”

However, the objects themselves have types as well. the object that lst points to is of type SLList. Although this object is intrinsically an SLList (since it was declared as such), it is also a List61B, because of the “is-a” relationship we explored earlier. But, because the object itself was instantiated using the SLList constructor, We call this its “dynamic type”.

Aside: the name “dynamic type” is actually quite semantic in its origin! Should lst be reassigned to point to an object of another type, say a AList object, lst’s dynamic type would now be AList and not SLList! It’s dynamic because it changes based on the type of the object it’s currently referring to.

当 Java 运行一个被覆盖的方法时，它会在其动态类型中搜索适当的方法签名并运行它。

Interface Inheritance VS Implement Inheritance

二者的区别与优劣如何？我这里直接摘录教材原文——

  • Interface inheritance (what): Simply tells what the subclasses should be able to do.
    • EX) all lists should be able to print themselves, how they do it is up to them.
  • Implementation inheritance (how): Tells the subclasses how they should behave.
    • EX) Lists should print themselves exactly this way: by getting each element in order and then printing them.

When you are creating these hierarchies, remember that the relationship between a subclass and a superclass should be an “is-a” relationship. AKA Cat should only implement Animal Cat is an Animal. You should not be defining them using a “has-a” relationship. Cat has-a Claw, but Cat definitely should not be implementing Claw.

Finally, Implementation inheritance may sound nice and all but there are some drawbacks:

  • We are fallible humans, and we can’t keep track of everything, so it’s possible that you overrode a method but forgot you did.
  • It may be hard to resolve conflicts in case two interfaces give conflicting default methods.
  • It encourages overly complex code

Week 4

By：思源南路世一劈

7 月 4 日

第四周……嗯，其实是第四天(雾)，这几天进度拉的有点快，需要放慢节奏了

目前计划是先肝到 Week 5，然后补掉前面的所有 discs，同时开始写 proj1，预计 7/7 前收掉

这样 CS61B 的内容大概就肝完 40%了，接下来迈入数据结构领域的同时迎接这个超大的挑战：Gitlet！(即 proj2)

预计在 7/14 前(即去成都之前)把 proj2 的进度推到 60%，7/20 前彻底收掉

这样剩余的部分基本就是一些编程哲学类的视频，预计 7/25 前彻底收尾

备注：proj3 应该是不写的，除非我能找到队友，收掉 61B 后着手预习电路理论，ICS 与离散数学(当然不可能都学，学一些是一些吧)！

至于交大教材版本的 ds，我的打算是跟着课本敲熟悉一遍代码，然后考虑刷点力扣熟悉 STL，保证开学之前拥有跟得上软工大二的码力(虽然我没选 SEP)

Inheritance and Implements

(续 Week 3 部分)

Extends

之前我们讲到类可以继承 interface ，这里的继承方式又分为实现继承与接口继承(而前者是有风险的)，那么类想要继承类该怎么办呢？

使用 extend 关键字，即可实现对类的继承，这里的继承可类比 C++里的 public 继承，但是没有 C++里面类型那么多，一个典型的例子如下(接续 Week 3 中提到的两种继承自 List61B 的 Lists)：

1
public class RotatingSLList<Item> extends SLList<Item>

关系图如下所示：

img

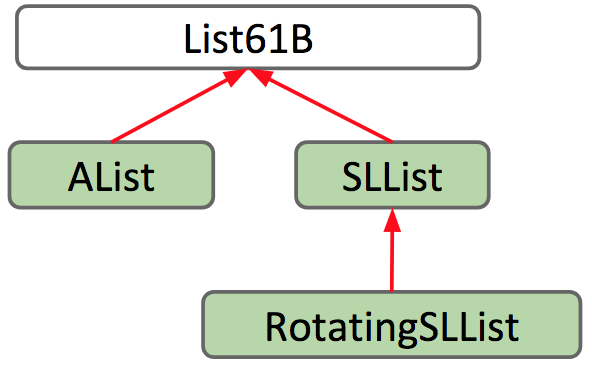
通过使用 extends 关键字，子类继承父类的所有成员。”成员”包括：

  • All instance and static variables
  • All methods
  • All nested classes

构造函数不会被继承，私有成员不能被子类直接访问

Object class

Java 中的所有类都是 Object 的后代，或也可以说成”是 Object 类”(is-a)

Object 类提供了很多基本的方法，例如toString() ， equals() 等，可以选择重写也可以选择不重写

Type Checking and Casting

Java 在编译时进行类型检查，此处检查时的依据是静态类型而不是动态类型，因此在代码中有时候会有必要添加显式的”强制类型转换”来告诉编译器这个地方该讲什么什么东西视作什么什么东西，例如：

1
Poodle largerPoodle = (Poodle) maxDog(frank, frankJr); // compiles! Right hand side has compile-time type Poodle after casting

但是类型转换也有风险，正如货币天然是金银，但金银天然不是货币，可能会引发类型转换错误：

1
2
3
4
Poodle frank = new Poodle("Frank", 5);
Malamute frankSr = new Malamute("Frank Sr.", 100);

Poodle largerPoodle = (Poodle) maxDog(frank, frankSr); // runtime exception!

在这种情况下，我们比较一只贵宾犬和一只马拉穆特犬。如果没有进行强制转换，编译器通常不会允许调用 maxDog 进行编译，因为右侧的编译时类型将是 Dog，而不是 Poodle。然而，强制转换允许这段代码通过，当 maxDog 在运行时返回马拉穆特犬时，我们尝试将马拉穆特犬强制转换为贵宾犬时，会遇到一个运行时异常 - 一个 ClassCastException

Inheritance Cheatsheet

VengefulSLList extends SLList 表示 VengefulSLList “是” SLList，并继承了 SLList 的所有成员：

  • Variables, methods nested classes
  • Not constructors Subclass constructors must invoke superclass constructor first. The super keyword can be used to invoke overridden superclass methods and constructors.

覆盖方法的调用遵循两个简单规则：

  • Compiler plays it safe and only allows us to do things according to the static type.
  • For overridden methods (not overloaded methods), the actual method invoked is based on the dynamic type of the invoking expression
  • Can use casting to overrule compiler type checking.

HoF and Subtype Polymorphism

这一节讲的主要是高阶函数以及子类的多态性

Java 中没有 Python 中那般方便的函数参数，也没有 JavaScript 里的回调函数，亦没有 C++里的函数指针

那么在 Java 中，该如何实现高阶函数的操作呢？答案是使用类继承的模式来书写，即使这样十分冗长。这是因为 Java 是纯面向对象编程的语言。

在了解到 HoF 的书写模式后，进一步深入，我们便得到了类似 C++里面类似”运算符重载”的操作，这在下一节，即可迭代对象与迭代器里又有着新的应用

Higher Order Functions

编写一个接口，定义任何接受整数并返回整数的函数 - 一个 IntUnaryFunction 。

1
2
3
public interface IntUnaryFunction {
    int apply(int x);
}

现在我们可以编写一个类， implements IntUnaryFunction 以表示一个具体的函数。让我们创建一个函数，该函数接受一个整数并返回该整数的 10 倍

1
2
3
4
5
6
public class TenX implements IntUnaryFunction {
    /* Returns ten times the argument. */
    public int apply(int x) {
        return 10 * x;
    }
}

此时，我们已经用 Java 编写了 tenX 函数的 Python 等价函数。现在让我们写 do_twice ：

1
2
3
public static int do_twice(IntUnaryFunction f, int x) {
    return f.apply(f.apply(x));
}

在 Java 中，对 print(do_twice(tenX, 2)) 的调用将如下所示：

1
System.out.println(do_twice(new TenX(), 2));

事实上，这里的接口扮演的角色即可以类比为 C++里的函数指针，而在实际调用时候的 new Tenx() 参数也可以换成其他的 subclass，以便于实现不同函数效果，为此我们只需要为不同的 subclass 写出不同的 apply 方法即可

Polymorphism

多态性，指的是对象可以具有多种形式或类型。在面向对象编程中，多态性涉及对象如何被视为其自身类的实例，其超类的实例，其超类的超类的实例等

考虑一个静态类型为 Deque 的变量 deque 。在执行时，调用 deque.addFirst() 将取决于 addFirst 被调用时 deque 的运行时类型或动态类型。正如我们在上一章中看到的，Java 使用动态方法选择来决定调用哪个方法

从狗狗们的故事引入————

还是以一直陪伴我们的 Dog 类为例，现在我想写一个函数 maxDog，给出两条狗里更大的那一条：

1
2
3
4
5
6
public Dog maxDog(Dog d1,Dog d2){
	if (d1 > d2)
        return d1;
    else
        return d2;
}

暗藏玄坤！大于号是可以用的吗？这里很显然会出问题，我们需要对 Dog 类的比较方法进行一个定义

考虑从现有接口 Comparable 继承，这是来自 Java 的内置接口，用来实现比较功能：

img

1
2
3
4
5
6
public class Dog implements Comparable<Dog> {
    ...
    public int compareTo(Dog uddaDog) {
        return this.size - uddaDog.size;
    }
}

上面的OurComparable是我们自己实现的可比较对象的接口，但是显然没有官方的完善

由此便实现了类似 C++中对“<,>”符号的运算符重载，只不过是 Java 特色重载

那么，如果我不想按照 size 的大小比较狗狗，而是按照狗狗名字的首字母顺序来给狗狗比较大小，又该怎么办呢？

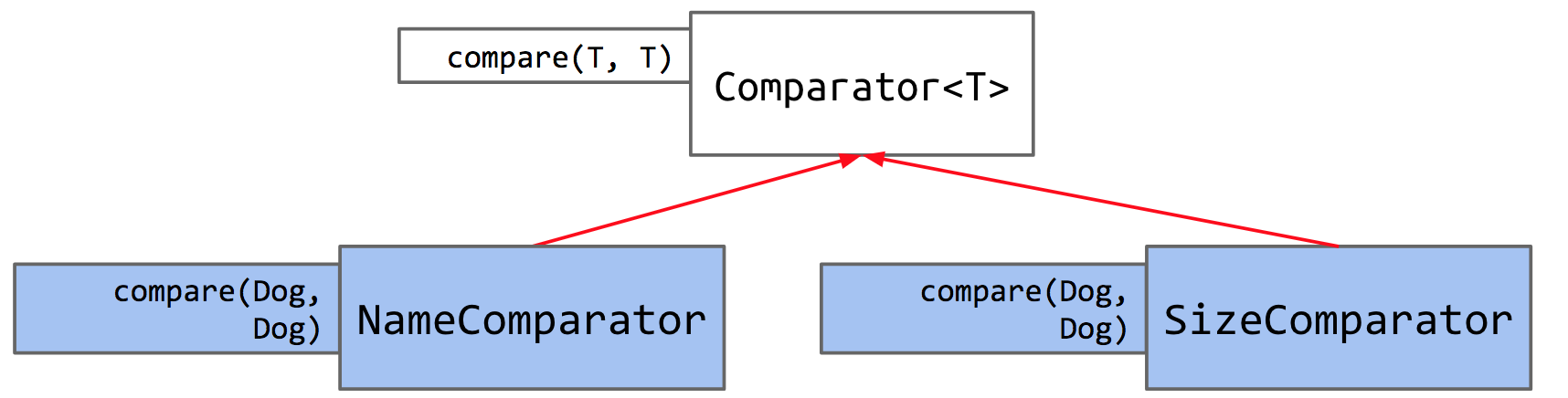
也就是说，我需要实现多种不同的比大小方法时该怎么办？引出我们的第二位兄弟：Comparator。Java 这样做的方式是通过使用 Comparator 。由于比较器是一个对象，我们将使用 Comparator 的方式是在 Dog 内编写一个实现 Comparator 接口的嵌套类，该接口的内容如下：

1
2
3
public interface Comparator<T> {
    int compare(T o1, T o2);
}

这表明 Comparator 接口要求任何实现类实现 compare 方法。 compare 的规则就像 compareTo ：

  • Return negative number if o1 < o2.
  • Return 0 if o1 equals o2.
  • Return positive number if o1 > o2.

实现的完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import java.util.Comparator;

public class Dog implements Comparable<Dog> {
    ...
    public int compareTo(Dog uddaDog) {
        return this.size - uddaDog.size;
    }

    private static class NameComparator implements Comparator<Dog> {
        public int compare(Dog a, Dog b) {
            return a.name.compareTo(b.name);
        }
    }

    public static Comparator<Dog> getNameComparator() {
        return new NameComparator();
    }
}

Note that we’ve declared NameComparator to be a static class. A minor difference, but we do so because we do not need to instantiate a Dog to get a NameComparator. Let’s see how this Comparator works in action.

img

也是让鼠鼠大开眼界！

Exceptions，Iterators，Iterables，Object Methods

进入下一部分，这一部分主要是一些 Java 语法知识的补充，包括异常、迭代、对象方法，了解完毕这些之后，CS61B 的第一部分(即 Java 的学习)也就宣告结束了(得益于自己 CPP 的底子，不然这些东西学起来不可能这么快······)

Exceptions

异常会导致正常的控制流停止。实际上，我们可以选择抛出自己的异常。在 Python 中，您可能已经看到过这种情况，使用 raise 关键字。在 Java 中，异常是对象，我们使用以下格式抛出异常：

1
throw new ExceptionObject(parameter1, ...)

一个典型例子如下：

1
2
3
4
5
6
7
8
9
10
11
12
/* Associates the specified value with the specified key in this map.
   Throws an IllegalArgumentException if the key is null. */
public void add(T x) {
    if (x == null) {
        throw new IllegalArgumentException("can't add null");
    }
    if (contains(x)) {
        return;
    }
    items[size] = x;
    size += 1;
}

为什么这么做？以下是课本原文，我做如下摘抄：

We get an Exception either way - why is this better?

  1. We have control of our code: we consciously decide at what point to stop the flow of our program
  2. More useful Exception type and helpful error message for those using our code

However, it would be better if the program doesn’t crash at all. There are different things we could do in this case. Here are some below:

Approach 1: Don’t add null to the array if it is passed into add

Approach 2: Change the contains method to account for the case if items[i] == null.

Whatever you decide, it is important that users know what to expect. That is why documentation (such as comments about your methods) is very important.

Iterators and Iterables

迭代器与可迭代对象。这部分内容实际上就是 python 中迭代器的概念加上上文提到的用 Java 实现比较器的手段

相关的接口代码如下：

1
2
3
public interface Iterable<T> {
    Iterator<T> iterator();
}
1
2
3
4
public interface Iterator<T> {
    boolean hasNext();
    T next();
}

在此基础上我们实现了可迭代版本的 Arraysets，完整的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
import java.util.Iterator;

public class ArraySet<T> implements Iterable<T> {
    private T[] items;
    private int size; // the next item to be added will be at position size

    public ArraySet() {
        items = (T[]) new Object[100];
        size = 0;
    }

    /* Returns true if this map contains a mapping for the specified key.
     */
    public boolean contains(T x) {
        for (int i = 0; i < size; i += 1) {
            if (items[i].equals(x)) {
                return true;
            }
        }
        return false;
    }

    /* Associates the specified value with the specified key in this map.
       Throws an IllegalArgumentException if the key is null. */
    public void add(T x) {
        if (x == null) {
            throw new IllegalArgumentException("can't add null");
        }
        if (contains(x)) {
            return;
        }
        items[size] = x;
        size += 1;
    }

    /* Returns the number of key-value mappings in this map. */
    public int size() {
        return size;
    }

    /** returns an iterator (a.k.a. seer) into ME */
    public Iterator<T> iterator() {
        return new ArraySetIterator();
    }

    private class ArraySetIterator implements Iterator<T> {
        private int wizPos;

        public ArraySetIterator() {
            wizPos = 0;
        }

        public boolean hasNext() {
            return wizPos < size;
        }

        public T next() {
            T returnItem = items[wizPos];
            wizPos += 1;
            return returnItem;
        }
    }

    public static void main(String[] args) {
        ArraySet<Integer> aset = new ArraySet<>();
        aset.add(5);
        aset.add(23);
        aset.add(42);

        //iteration
        for (int i : aset) {
            System.out.println(i);
        }
    }

}

Object Methods

如上文所述，Java 中所有的类都是 Object 类的子类，也可以说 Object 是最顶端的 superclass，继承的方法如下：

  • String toString()
  • boolean equals(Object obj)
  • Class <?> getClass()
  • int hashCode()
  • protected Objectclone()
  • protected void finalize()
  • void notify()
  • void notifyAll()
  • void wait()
  • void wait(long timeout)
  • void wait(long timeout, int nanos)

这里专注理解前两个即可

toString()

相当于将某个对象字符串化的时候该怎么办？toString()解决的就是这个问题

equals()

注意，Java 中 == 在比较对象的时候实际上比较的是二者是否是同一个对象，即二者存储的地址是否相同。而这显然不符合特定情况下我们的要求，所以我们采取 equals 来重载我们的 =

7 月 6 日

牛魔，计划有变，估计要到 8 号才能写完 proj1 了

7 月 7 日

补充一个继承的知识点：

  • 不能用 super.super.something 的方式来调用父类的父类，因为你只能有一个爹

补充一个动态方法选择：

  • 编译时，在其静态类型中查看有无合适的签名，若有则锁定该签名，否则 Compile Error
  • 运行时，在锁定签名的前提下，再在其动态类型查找有无更合适的方法，若无，则进一步查询其父类

Week 5

无事发生

Week 6

7 月 9 日

经过 7、8 二日的奋斗，终于写完了 Project 1，今天先续上前面的 Week 6

今天的内容主要是算法运行时间分析、不相交集合、ADTs(即抽象数据类型，主要介绍了 Map, Stack, BST 并基本实现了二叉搜索树 BST)

Efficient Programming

名字很洋气，但是其实就是算法的运行时间分析。先扔一个符号的定义表格：

Signals Informal Meaning Example Family
Big Theta Θ(𝑓(𝑁)) Order of growth is f(N) Θ(𝑁)
Big O 𝑂(𝑓(𝑁)) Order of growth is less than or equal to f(N) 𝑂(𝑁)
Big Omega Ω(𝑓(𝑁)) Order of growth is greater than or equal to f(N) Ω(𝑁)

然后我只需要列举一些常见的复杂度例子即可：

  • N：单层遍历循环
  • N^2：双层遍历循环
  • log N：二分查找
  • N log N：归并排序

Disjoint Sets

一个不相交集数据结构有固定数量的元素，每个元素最初都在自己的子集中。通过调用 connect(x, y) 来合并一些元素 x 和 y 的子集。

不相交集合主要有两种操作：

  • connect(x, y) ：连接 x 和 y 。又称为 union
  • isConnected(x, y) ：如果 x 和 y 连接（即属于同一集合），则返回 true

一些操作示例如下图所示：

假设我们有四个元素，称为 A、B、C、D。首先，每个元素都在自己的集合中：

img

在调用 connect(A, B) 后：

img

1
2
isConnected(A, B) -> true
isConnected(A, C) -> false

在调用 connect(A, D) 后：

img

We find the set A is part of and merge it with the set D is part of, creating one big A, B, D set. C is left alone.
我们发现集合 A 是部分的，并将其与集合 D 是部分的合并，创建一个大的 A、B、D 集合。C 保持不变。
isConnected(A, D) -> true
isConnected(A, C) -> false

直观地，我们可能首先考虑将不相交集表示为一组集合，例如， List<Set<Integer>> 。但是这样对于一个很长的链表而言，查找与判断是否连接都将非常困难，并且在代码实现上也具有相当的难度，因此我们舍弃

接下来，我们从一步步优化这个数据结构入手，来探究不相交集合是怎样实现的：

Quick Find

蛤！我们进行第一次优化，将不相交集合用数组的方式来实现

  • The indices of the array represent the elements of our set.
  • The value at an index is the set number it belongs to.

例如，我们将 {0, 1, 2, 4}, {3, 5}, {6} 表示为：

img

这样一来，若想要连接某两个元素，只需要将其 id 修改为同一个数字即可

对于判断是否链接，也只需要检测这两个位置的 id 是否相同即可，时间复杂度是 Θ(1)！

但是构造函数与 connect(x,y) 需要的时间复杂度依然是 Θ(N)，我们继续······

相关代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public class QuickFindDS implements DisjointSets {

    private int[] id;

    /* Θ(N) */
    public QuickFindDS(int N){
        id = new int[N];
        for (int i = 0; i < N; i++){
            id[i] = i;
        }
    }

    /* need to iterate through the array => Θ(N) */
    public void connect(int p, int q){
        int pid = id[p];
        int qid = id[q];
        for (int i = 0; i < id.length; i++){
            if (id[i] == pid){
                id[i] = qid;
            }
        }
    }

    /* Θ(1) */
    public boolean isConnected(int p, int q){
        return (id[p] == id[q]);
    }
}

Quick Union

我们继续优化，用近似树的结构来描述每一个集合：

不再使用 id，而是为每个项目分配其父项的索引。如果一个项目没有父项，那么它就是一个“根”，我们为其分配一个负值

这种方法使我们能够将我们的每个集合想象成一棵树。例如，我们将 {0, 1, 2, 4}, {3, 5}, {6} 表示为：

img

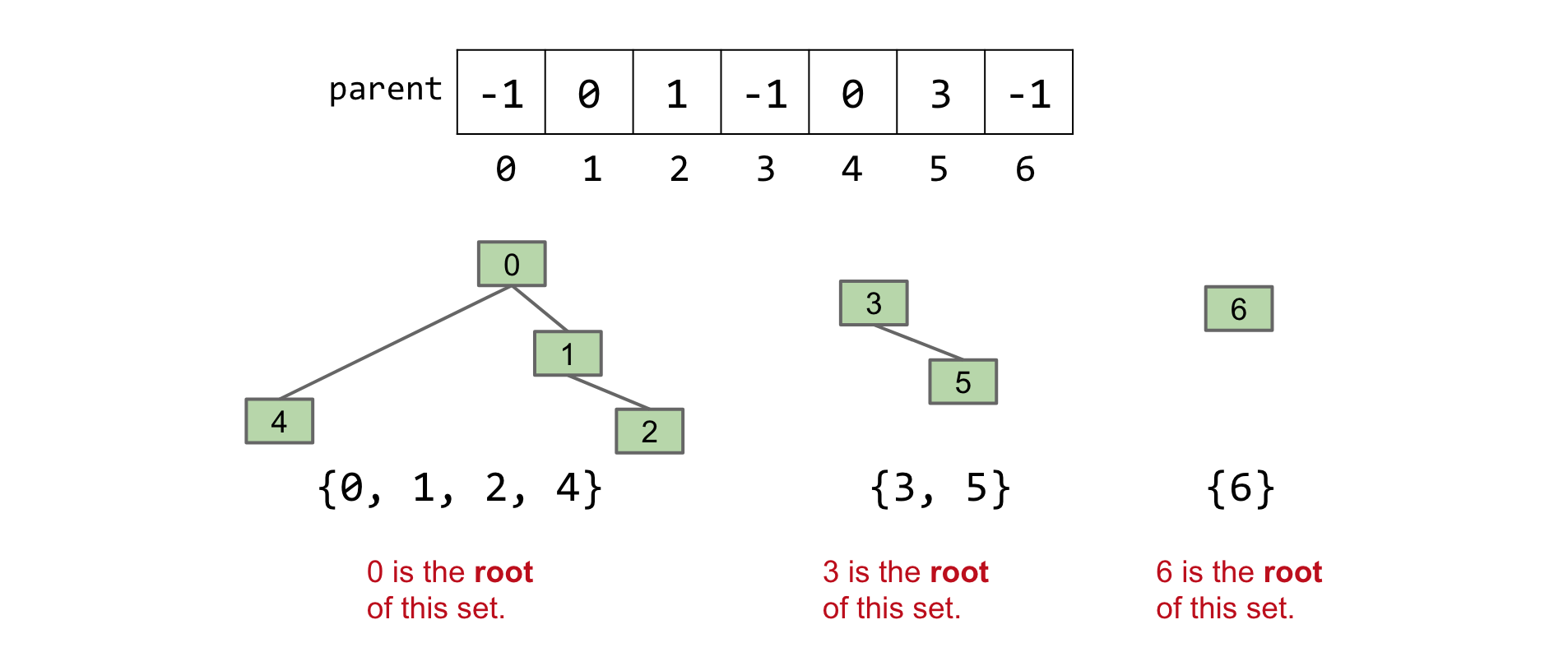
对于 QuickUnion，我们定义一个辅助函数 find(int item) ，它返回树 item 所在的根。例如，对于上面的集合， find(4) == 0 ， find(1) == 0 ， find(5) == 3 等。每个元素都有一个唯一的根。

这样一来，对于 connect(x,y) 函数，我们需要做的即是将 y 的根节点设置为 x 的根结点的子节点

对于 isConnected(x,y) 函数，我们需要做的即为找到二者的根节点并判断它们是否相等

注意到此时算法的性能将完全取决与 find(X) 的性能：当树很平缓时，二者性能都较为优良，当树狭长而高耸时，二者性能将退化为 N 的水平，因此这二者的时间复杂度都是 O(N)

是不是看起来像倒退了？但是注意这里的 O 符号表示的是小于等于，而我们只要控制好树的形状，便能尽量避免悲剧的发生，因此我们需要在 connect(x,y) 函数上继续下功夫

本小节的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public class QuickUnionDS implements DisjointSets {
    private int[] parent;

    public QuickUnionDS(int num) {
        parent = new int[num];
        for (int i = 0; i < num; i++) {
            parent[i] = i;
        }
    }

    private int find(int p) {
        while (parent[p] >= 0) {
            p = parent[p];
        }
        return p;
    }

    @Override
    public void connect(int p, int q) {
        int i = find(p);
        int j= find(q);
        parent[i] = j;
    }

    @Override
    public boolean isConnected(int p, int q) {
        return find(p) == find(q);
    }
}

Weighted Quick Union (WQU)

新规则：每当我们调用 connect 时，我们总是将较小树的根链接到较大树

遵循这个规则将使您的树的最大高度为 log𝑁logN ，其中 N 是我们不相交集中元素的数量

让我们通过一个例子来说明这个好处。考虑连接下面的两个集合 T1 和 T2：

img

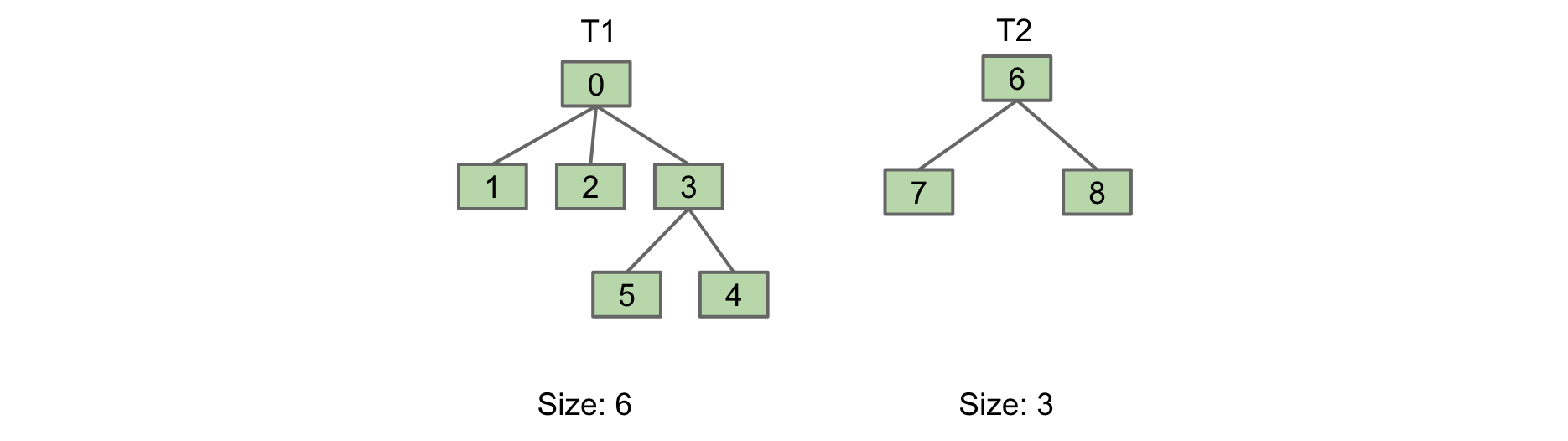
我们有两种选项可以连接它们：

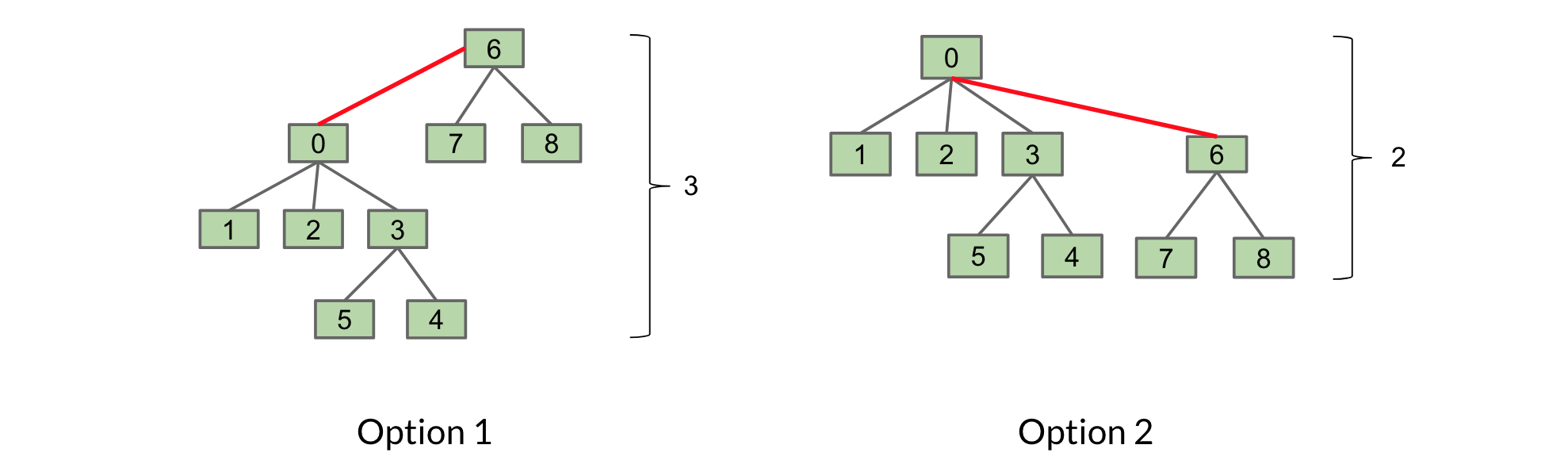img 第一个选项是我们将 T1 链接到 T2。在第二个选项中，我们将 T2 链接到 T1。

第二个选项更可取，因为它只有 2 的高度，而不是 3。根据我们的新规则，我们也会选择第二个选项，因为 T2 比 T1 小（3 与 6 的大小相比）。

我们通过树中的项目数量来确定大小。因此，连接两棵树时，我们需要知道它们的大小（或权重）。我们可以将这些信息存储在树的根部，通过用 -(size of tree) 替换 -1

还能继续优化吗？答案是可以，我们可以在按权重 connect 的同时进一步优化树的结构

Weighted Quick Union with Path Compression

无论何时我们调用 find(x) ，我们都必须从 x 遍历到根。因此，在这个过程中，我们可以将所有访问的项目连接到它们的根，而不会增加额外的时间成本

将沿途所有项目连接到根部将有助于使我们的树在每次调用 find 时更短

注意到 connect(x, y) 和 isConnected(x, y) 总是调用 find(x) 和 find(y) 。因此，在调用足够多次 connect 或 isConnected 之后，基本上所有元素将直接指向它们的根。

通过推广， connect 和 isConnected 的平均运行时间在长期内几乎保持恒定！

Summary

总结如下：

N: number of elements in Disjoint Set

Implementation isConnected connect
Quick Find Θ(N) Θ(1)
Quick Union O(N) O(N)
Weighted Quick Union (WQU) O(log N) O(log N)
WQU with Path Compression O(α(N))* O(α(N))*

ADTs

这一节主要介绍了一些抽象数据结构，抽象数据类型（ADT）仅由其操作定义，而不是由其实现定义。

Abstract data types (ADTs) are defined in terms of operations, not implementation.

Several useful ADTs:

  • Disjoint Sets, Map, Set, List.
  • Java provides Map, Set, List interfaces, along with several implementations.

同时，本章简单实现了一下二叉搜索树 BST。这里针对后者记录一下

BST(二叉搜索树)

先给出树的一般定义：

Trees are composed of:

  • nodes
  • edges that connect those nodes.
    • Constraint: there is only one path between any two nodes.

In some trees, we select a root node which is a node that has no parents.

A tree also has leaves, which are nodes with no children.

进一步我们有二叉树和二叉搜索树的定义：

  • Binary Trees: in addition to the above requirements, also hold the binary property constraint. That is, each node has either 0, 1, or 2 children.
  • Binary Search Trees: in addition to all of the above requirements, also hold the property that For every node X in the tree:
    • Every key in the left subtree is less than X’s key.
    • Every key in the right subtree is greater than X’s key. Remember this property!! We will reference it a lot throughout the duration of this module and 61B.

Here is the BST class we will be using in this module:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
private class BST<Key> {
    private Key key;
    private BST left;
    private BST right;

    public BST(Key key, BST left, BST Right) {
        this.key = key;
        this.left = left;
        this.right = right;
    }

    public BST(Key key) {
        this.key = key;
    }
}

可以将 BST 视作是有序的二叉树，这在搜索的时候非常方便与迅速

BST 的功能

类比二分查找，当我们想要查找 BST 中的数据的时候，思路是同样的：

  • 和当前结点的值比大小，若是则返回
  • 若是小于待查值，则往右拐
  • 若是大于待查值，则往左拐

速度贼快！如果树很茂密，那么树的高度 H = log N，即意味着查找用时也是 log N

Insert

对于插入，总体思路和查找相似，代码如下：

1
2
3
4
5
6
7
8
9
static BST insert(BST T, Key ik) {
  if (T == null)
    return new BST(ik);
  if (ik ≺ T.key)
    T.left = insert(T.left, ik);
  else if (ik ≻ T.key)
    T.right = insert(T.right, ik);
  return T;
}
Delete

删除操作则需要分类讨论：

  • 被删除结点无子节点
  • 被删除结点有一个子节点
  • 被删除结点有两个子节点

若无子节点，直接删除即可

若有一个子节点，子承父业

若有两个子节点，选贤者任之——即选择一个新节点替换之，那么怎么选择呢？
我们知道新节点必须:

  • be > than everything in left subtree.
  • be < than everything right subtree.

所以可以只需取左子树中最右边的节点或右子树中最左边的节点，然后把它放到待删除结点的位置即可！

Week 7

7 月 10 日

今天看完了 Week 7 的内容，主要内容包括两方面：一是对 BST 的进一步深化探究：B 树，红黑树；另一方面是对哈希(Hashing)的介绍，主要从如何实现高效的哈希表入手，并一步步优化更改，直到贴近实际的实现

Balanced Trees

本章标题叫做”平衡树”，何谓平衡？我们知道，二叉搜索树虽然方便，但是其实际效能却取决于其结构：

Worst case: Θ(𝑁)

Best-case: Θ(log𝑁) (where 𝑁N is number of nodes in the tree)

于是引入 BST 性能的一些术语：

  • depth: the number of links between a node and the root.
  • height: the lowest depth of a tree.
  • average depth: average of the total depths in the tree.

树的高度决定了最坏情况的运行时间，因为在最坏情况下，我们要查找的节点位于树的底部。

平均深度决定了平均情况下的运行时间。

B-Trees

进入 B 树的领域！

B 树为什么叫这个名字视频中也没有提及，或许是因为 Balanced 的意义吧

牢 Josh 引入这个 B 树的想法还是相当疯狂的——

既然不想让高度太高，那我就不准插入子节点！但是这显然又是不行的，于是我们进一步修改，例如限制每个结点的数据数量，假设是 4，那么这时候插入结点的操作如下：

  1. We still always inserting into a leaf node, so take the node you want to insert and traverse down the tree with it, going left and right according to whether or not the node to be inserted is greater than or smaller than the items in each node.
  2. After adding the node to the leaf node, if the new node has 4 nodes, then pop up the middle left node and re-arrange the children accordingly.
  3. If this results in the parent node having 4 nodes, then pop up the middle left node again, rearranging the children accordingly.
  4. Repeat this process until the parent node can accommodate or you get to the root.

事实上，这时候树的建造过程就是”自下而上”的，这样自然也就保证了得到的树是自平衡的！进而保证了其 log N 的优异性能

这是一个很好用的 B 树可视化工具：

B-Tree Visualization (usfca.edu)

B-Trees Invariants

B-树具有以下有用的不变性：

  • All leaves must be the same distance from the source.
  • A non-leaf node with 𝑘 items must have exactly 𝑘+1 children.

In tandem, these invariants cause the tree to always be bushy.

发现没有，如果我们通过数据结构的教材自学，那么它一上来给我们的就是这样枯燥的东西，自然学懂起来就会复杂许多，而通过牢 Josh 这样生动丰富的讲解，才能让我们做到知其然亦知其所以然

Rotating Trees

尽管 B 树性能优越，但实现起来却十分困难

为了让普通的 BST 也能实现平衡结构，我们引出旋转树的操作

旋转的正式定义是：

1
2
rotateLeft(G): Let x be the right child of G. Make G the new left child of x.
rotateRight(G): Let x be the left child of G. Make G the new right child of x.

理解上，可以将旋转的过程视作先将两个结点合并，再将原结点”发射”到另一侧的过程

相关代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
private Node rotateRight(Node h) {
    Node x = h.left;
    h.left = x.right;
    x.right = h;
    return x;
}

private Node rotateLeft(Node h) {
    Node x = h.right;
    h.right = x.left;
    x.left = h;
    return x;
}

Red-Black Trees

利用树旋转，我们最终来到红黑树——通过 BST 的结构来模拟 B 树，实现代码的简洁，同时保证效率与性能

Here is a summary of all the operations:

  • When inserting: Use a red link.
  • If there is aright leaning “3-node”, we have a Left Leaning Violation
    • Rotate left the appropriate node to fix.
  • If there are two consecutive left links, we have an incorrect 4 Node Violation!
    • Rotate right the appropriate node to fix.
  • If there are any nodes with two red children, we have a temporary 4 Node.
    • Color flip the node to emulate the split operation.
Runtime

Because a left-leaning red-black tree has a 1-1 correspondence with a 2-3 tree and will always remain within 2x the height of its 2-3 tree, the runtimes of the operations will take log𝑁logN time.

Here’s the abstracted code for insertion into a LLRB:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
private Node put(Node h, Key key, Value val) {
    if (h == null) { return new Node(key, val, RED); }

    int cmp = key.compareTo(h.key);
    if (cmp < 0)      { h.left  = put(h.left,  key, val); }
    else if (cmp > 0) { h.right = put(h.right, key, val); }
    else              { h.val   = val;                    }

    if (isRed(h.right) && !isRed(h.left))      { h = rotateLeft(h);  }
    if (isRed(h.left)  &&  isRed(h.left.left)) { h = rotateRight(h); }
    if (isRed(h.left)  &&  isRed(h.right))     { flipColors(h);      }

    return h;
}

红黑树的删除过程较为繁琐，此处略去不谈

Hashing

经过我们从 BST-BT-LLRB 的不断优化，查询的运行用时已经被我们做到了 log N 的境界，那么，还能进一步变强吗？(或者以空间换时间？)

基本思路是直接使用数组来替代上面那么复杂的数据结构——以空间换时间！直接用数组的 index 代表数据，用 true/false 代表是否被存储——

  • 如何适用除数字以外的其他数据？——使用 ASCII！或者 Unicode！
  • 不可避免的冲突？——内部使用 List 结构！
  • 内存开销巨大？运行时不稳定？——使用限定大小且动态增长的数组！同时进一步改进我们的 Hashcode!

这样便得到我们的哈希表——

  • Inputs are converted by a hash function (hashcode) into an integer. Then, they’re converted to a valid index using the modulus operator. Then, they’re added at that index (dealing with collisions using LinkedLists).
  • contains works in a similar fashion by figuring out the valid index, and looking in the corresponding LinkedList for the item.

补充：哈希码具有三个必要属性，这意味着哈希码必须具备这些属性才能有效：

  1. It must be an Integer
  2. If we run .hashCode() on an object twice, it should return the same number
  3. Two objects that are considered .equal() must have the same hash code.

这样，在哈希码分布均匀的情况下，查找的时间便被限制在了 O(1)的级别！

Week 8

7 月 11 日

Week 8 内容比较杂，先讲了一种全新的数据结构——优先级队列(PQ)，使用二叉堆的结构。随后简单给图的部分开了个头，介绍了图的定义和基本 API。然后介绍并讲解了深度优先遍历(DFS)和广度优先遍历(BFS)，以及它们的基本实现

Heaps and Priority Queues

PQ Interfaces

和队列类似，优先级队列也可以添加/删除元素，但和普通队列不同的是，优先级队列只能让我们访问其最小(或最大)的元素，这在一些需要排序的场合具有重大作用，其接口一般如下所示：(以最小优先级队列为例)

1
2
3
4
5
6
7
8
9
10
11
12
/** (Min) Priority Queue: Allowing tracking and removal of
  * the smallest item in a priority queue. */
public interface MinPQ<Item> {
    /** Adds the item to the priority queue. */
    public void add(Item x);
    /** Returns the smallest item in the priority queue. */
    public Item getSmallest();
    /** Removes the smallest item from the priority queue. */
    public Item removeSmallest();
    /** Returns the size of the priority queue. */
    public int size();
}

如何实现？使用有序数组？BST？哈希表？各有优劣：

  • Ordered Array
    • add: Θ(𝑁)
    • getSmallest: Θ(1)
    • removeSmallest: Θ(𝑁)
  • Bushy BST
    • add: Θ(log𝑁)
    • getSmallest: Θ(log𝑁)
    • removeSmallest: Θ(log𝑁)
  • HashTable
    • add: Θ(1)
    • getSmallest: Θ(𝑁)
    • removeSmallest: Θ(𝑁)

可以做的更好吗？由此引申出我们的二叉堆——一种特殊的树结构，用于实现我们的优先级队列

Heaps

堆的基本定义如下：

  • 首先是一颗完整的二叉树
  • 每个结点的值小于等于其两个子节点的值(当然在求 max 的情况下反过来即可)
  • 所有结点尽量左倾

img

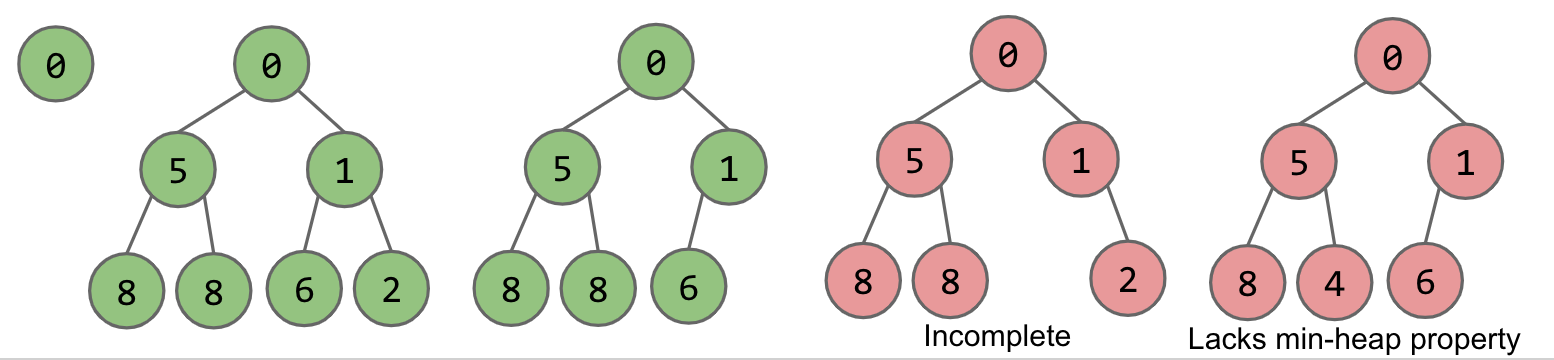
如上图所示：红色的即为不合规的堆
我们关心优先级队列的三种方法是 add ， getSmallest 和 removeSmallest 。

  • add: Add to the end of heap temporarily. Swim up the hierarchy to the proper place.
    • Swimming involves swapping nodes if child < parent
  • getSmallest: Return the root of the heap (This is guaranteed to be the minimum by our min-heap property
  • removeSmallest: Swap the last item in the heap into the root. Sink down the hierarchy to the proper place.
    • Sinking involves swapping nodes if parent > child. Swap with the smallest child to preserve min-heap property

可以发现，这里调整堆的结构的一种很重要的思想就是”上浮”以及”下沉”！那么如何实现这种操作呢？

使用树？数组？这里就不卖关子了，事实上，一种极为巧妙的思路就是利用数组的 id 为每个堆的元素标号，这样一来，每个结点的编号与其父结点的编号便有了数学上的关系：

  • leftChild(k)=𝑘∗2
  • rightChild(k)=𝑘∗2+1
  • parent(k) =𝑘/2

是不是很巧妙(doge)!

与其他的实现方式对比：

Methods Ordered Array Bushy BST Hash Table Heap
add Θ(𝑁) Θ(log𝑁) Θ(1)Θ(1) Θ(log𝑁)
getSmallest Θ(1) Θ(log𝑁) Θ(𝑁) Θ(1)
removeSmallest Θ(𝑁) Θ(log𝑁) Θ(𝑁) Θ(log𝑁)

DS Summary

对已经学习过的数据结构进行一个总结：

Name Store Operation(s) Primary Retrieval Operation Retrieve By
List add(key), insert(key, index) get(index) index
Map put(key, value) get(key) key identity
Set add(key) containsKey(key) key identity
PQ add(key) getSmallest() key order (aka key size)
Disjoint Sets connect(int1, int2) isConnected(int1, int2) two integer values

下一集——图！

Graph,DFS,BFS

其实这是两章的内容，但是我看牢 Josh 有点水课的嫌疑，所以放到一起了

先从树遍历讲起，然后引入图——

Tree Traversal

回想一下，还在列表那一集的时候我们讲到了迭代的概念，对于列表来说这一切是如此自然——只需要一步步往后走便是了，那么对于树来说呢？

一共有四种遍历的方式：层序，先序，顺序，后序(翻译是这样的，感觉英文更好理解一些)

Level Order Traversal

顾名思义，一层一层遍历，从第 0 层(即根节点)开始，一步步向后推·······

得到的结果是： D B F A C E G

Pre-order Traversal

先序遍历，简记：我最大！然后左右

代码如下：

1
2
3
4
5
6
preOrder(BSTNode x) {
    if (x == null) return;
    print(x.key)
    preOrder(x.left)
    preOrder(x.right)
}

得到的结果是：D B A C F E G

In-order Traversal

顺~序遍历，严格按照左中右的方式执行，这也是按顺序打印 BST 内容的方法

代码如下：

1
2
3
4
5
6
inOrder(BSTNode x) {
    if (x == null) return;
    inOrder(x.left)
    print(x.key)
    inOrder(x.right)
}

得到的结果是：A B C D E F G

Post-order Traserval

后序遍历——以大局为重！先集体后个人()

代码如下：

1
2
3
4
5
6
postOrder(BSTNode x) {
    if (x == null) return;
    postOrder(x.left)
    postOrder(x.right)
    print(x.key)
}

得到的结果是：A C B E G F D

Graph

开图！

什么是图？还记得树的定义吗？我们要求树里面任意两个结点之间有且仅有一条路径，在图里，没有这个限制

也就是说，所有的树都是图！下面给出图的定义：

A graph consists of:

  • A set of nodes (or vertices)
  • A set of zero of more edges, each of which connects two nodes.

图的分类很多，有向图/无向图，简单图/复杂图，非循环图/循环图，加权图···等等，这里我们只研究简单图

Basic Problems

图研究的主要问题有：(英语太差，所以双语都放上来)

  • s-t Path: Is there a path between vertices s and t?
    s-t 路径：顶点 s 和 t 之间是否有路径？
  • Connectivity: Is the graph connected, i.e. is there a path between all vertices?
    连通性：图是否连通，即所有顶点之间是否存在路径？
  • Biconnectivity: Is there a vertex whose removal disconnects the graph?
    双连通性：是否存在一个顶点，其移除会使图断开连接？
  • Shortest s-t Path: What is the shortest path between vertices s and t?
    最短 s-t 路径：顶点 s 和 t 之间的最短路径是什么？
  • Cycle Detection: Does the graph contain any cycles?
    循环检测：图中是否包含任何循环？
  • Euler Tour: Is there a cycle that uses every edge exactly once?
    欧拉循环: 是否存在一个使用每条边恰好一次的循环？
  • Hamilton Tour: Is there a cycle that uses every vertex exactly once?
    汉密尔顿循环：是否有一个循环，每个顶点恰好使用一次？
  • Planarity: Can you draw the graph on paper with no crossing edges?
    平面性：您能否在纸上绘制图形而不交叉边缘？
  • Isomorphism: Are two graphs isomorphic (the same graph in disguise)?
    同构：两个图同构（伪装成相同的图）？

以第一个问题为例，我们可以引申出 DFS 和 BFS

深度优先搜索！不撞南墙不回头！

具体思路是：

  • 对于当前结点，先标记之
  • 判断当前结点是否是目标结点，是则返回
  • 对于该结点没有被标记的邻居结点，递归调用(否则会死循环)
  • 若没有这样的邻居结点，则返回 False

伪代码：

1
2
3
4
5
6
7
8
9
mark s  // i.e., remember that you visited s already
if (s == t):
    return true;

for child in unmarked_neighbors(s): // if a neighbor is marked, ignore!
    if isconnected(child, t):
        return true;

return false;

广度优先搜索！优先拿离自己进的人开 🔪！

具体思路：在 DFS 的基础之上，增加一个数组来跟踪哪些结点接下来将被调查！例如我们到达一个结点，在判断该结点的情况后，就标记该结点，再这个结点的非标记邻居拉近审查名单，随后审查名单便会动态增长或缩短，直到我们找到目的或者找遍整个图

BFS 的伪代码如下：

1
2
3
4
5
6
7
8
Initialize the fringe (a queue with the starting vertex) and mark that vertex.
Repeat until fringe is empty:
Remove vertex v from the fringe.
For each unmarked neighbor n of v:
Mark n.
Add n to fringe.
Set edgeTo[n] = v.
Set distTo[n] = distTo[v] + 1.

A fringe is just a term we use for the data structure we are using to store the nodes on the frontier of our traversal’s discovery process (the next nodes it is waiting to look at). For BFS, we use a queue for our fringe.

edgeTo[...] is a map that helps us track how we got to node n; we got to it by following the edge from v to to n.

distTo[...] is a map that helps us track how far n is from the starting vertex. Assuming that each edge is worth a distance of 1, then the distance to n is just one more than the distance to get to v. Why? We can use the way we know how to get to v, then pay one more to arrive at n via the edge that necessarily exists between v and n (it must exist since in the for loop header, n is defined as a neighbor of v).

Representing Graphs

1
2
3
4
5
6
7
public class Graph {
  public Graph(int V):               // Create empty graph with v vertices
  public void addEdge(int v, int w): // add an edge v-w
  Iterable<Integer> adj(int v):      // vertices adjacent to v
  int V():                           // number of vertices
  int E():                           // number of edges
...

Week 9

7 月 12 日-7 月 15 日

这几天摆了，主要原因是瞌睡太多(雾)，断断续续看了 Week 9 和 Week 10 的部分内容，这里记录一下 Week 9

Week 9 一方面是对图的内容进行了进一步的深入探讨，两方面：最短路径与最小生成树；另一方面则简单介绍了多维数据与 K-D-Tree(没记错的话应该是 ads 里面的内容)。但是对于后者我不打算记笔记，仅作为参考了解

Shortest Paths

直接上干货吧，这没什么好引入的，主要内容重点是算法思想及其运行时，而非代码实现：

最短路径，即给定图中的任意两点，我们需要找到连接这两点之间的最短路径，这里的图有可能是加权图，即不同边的权重(a.k.a 长度)不一样。我们采用的方法主要有两种：**Dijkstra and A***，前者重在算无遗策，给出的答案绝对正确，而后者则是一种启发式算法，力求直捣黄龙，但是精度可能有影响！

Dijkstra

该算法的主要操作是：给你一个顶点，还你一颗最短路径树(即包含了该顶点到其他所有顶点的最短路径)

概括地说，该算法分三步走：

  • 创建一个 PQ，其内容即为各个顶点，对应的值时当前时刻每个顶点到源顶点的最短距离
  • 将初始点的值设为 0，其他的设置为正无穷
  • 当 PQ 非空时，弹出其顶点，并**放松(relax)**其所有边，直到 PQ 为空

放松，即对当前顶点的所有边进行一个距离的检查，如果当前顶点的距离加上该边的权重小于该边另一个顶点的距离，则更新之。这个计算潜在距离、检查是否更好并可能更新的整个过程被称为放松(relax)。

Important note: we never relax edges that point to already visited vertices. 所以不要忘记标记已经访问过的顶点，当某个顶点从 PQ 中弹出后，它就不会再次被访问

伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def dijkstras(source):
    PQ.add(source, 0)
    For all other vertices, v, PQ.add(v, infinity)
    while PQ is not empty:
        p = PQ.removeSmallest()
        relax(all edges from p)
def relax(edge p,q):
   if q is visited (i.e., q is not in PQ):
       return

   if distTo[p] + weight(edge) < distTo[q]:
       distTo[q] = distTo[p] + w
       edgeTo[q] = p
       PQ.changePriority(q, distTo[q])

该算法的证明如下：(摘抄自课本)

Assume all edges are non-negative.

  • At start, distTo[source] = 0. This is optimal.

  • After relaxing all edges from source, let vertex 𝑣1be the vertex with the minimum weight (i.e., the one that’s closest to the source.)Claim: distTo[𝑣1] is optimal, i.e., whatever the value of distTo[𝑣1] is at this point is the shortest distance from 𝑠s to 𝑣1.

    Why?

    • Let’s try to see why this MUST be the case.
    • Suppose that it isn’t the case. Then that means that there is some other path from 𝑠s to 𝑣1 which is shorter than the direct path (𝑠,𝑣1). Ok, so let’s consider this hypothetical cool shorter path… it would have to look like (𝑠,𝑣𝑎,𝑣𝑏,…,𝑣1). But… (𝑠,𝑣𝑎) is already bigger than (𝑠,𝑣1). (Note that this is true because 𝑣1 is the vertex that is closest to 𝑠 from above.) So how can such a path exist which is actually shorter? It can’t!

  • Now, the next vertex to be popped will be 𝑣1. (Why? Note that it currently has the lowest priority in the PQ!)

  • So now, we can make this same argument for 𝑣1 and all the relaxation it does. (This is called “proof by induction”. It’s kind of like recursion for proofs.) And that’s it; we’re done.

算法的局限性：边的权重必须非负！

A*

D 算法强调算无遗策，即我的探索路径类似一个同心圆，在抵达目标的同时事实上我也找到了同心圆里面的其他结点的所有最短路径，这似乎有点太城市化了？

如果能在 PQ 的排列中加上一点”方向性”就好了！即带有引导式的去引诱最短路径树的生长方向

事实上，我们只需要修改一下 D 算法：在 Dijkstra 算法中，我们使用 bestKnownDistToVbestKnownDistToV 作为算法中的 PQ 优先级。这一次，我们将使用 bestKnownDistToV+estimateFromVToGoalbestKnownDistToV+estimateFromVToGoal 作为我们的 PQ 优先级。

显然，如果这里的估计做的不好，显然算法的精度就会降低，但是如果估计做的好，那么该算法将拥有快于 D 算法的速度和更高的效率，显然更加美妙！例如在地图里寻找两个城市间的最短路径时，我们便可以采用两点间的直线距离来作为一个暂时的估计

这里是一个 A*算法演示： demo

关于估计的要求，摘自教材：

The takeaway here is that heuristics need to be good. There are two definitions required for goodness.

  1. Admissibility. heuristic(v, target) ≤ trueDistance(v, target). (Think about the problem above. The true distance from the neighbor of 𝐶 to 𝐶 wasn’t infinity, it was much, much smaller. But our heuristic said it was ∞∞, so we broke this rule.)
  2. Consistency. For each neighbor 𝑣 of 𝑤:
    • heuristic(v, target) ≤ dist(v, w) + heuristic(w, target)
    • where dist(v, w) is the weight of the edge from v to w.
      )

demo 详见：cs61b 2020 lec 25 shortest paths - Google 幻灯片

Minimum Spanning Trees

Definition

最小生成树：指包含了图中所有结点的且总路径和最短的一棵树。当然这是我的理解，原文如下：

A minimum spanning tree (MST) is the lightest set of edges in a graph possible such that all the vertices are connected. Because it is a tree, it must be connected and acyclic. And it is called “spanning” since all vertices are included.

Cut

我们可以将切割定义为将图的节点分配给两个非空集合的过程(即我们将每个节点分配给集合一或集合二)。

我们可以将横跨边定义为连接一个集合中的节点与另一个集合中的节点的边。

有了这两个定义，我们就可以理解切割属性；给定任何切割，最小权重的横跨边在最小生成树中。

Prim’s Algorithm

类似 Dijkstra 算法，只是将到源顶点的距离换成到当前树的距离，核心思想：

1
2
3
1. Start from some arbitrary start node.
2. Repeatedly add the shortest edge that has one node inside the MST under construction.
3. Repeat until there are V-1 edges.

一个算法演示：CS61B Prim’s Demo - Google 幻灯片

Kruskal’s Algorithm

实现起来较为简单，使用 PQ 对所有边排序然后直接霸王硬上弓：

1
2
3
1. Sort all the edges from lightest to heaviest.
2. Taking one edge at a time (in sorted order), add it to our MST under construction if doing so does not introduce a cycle.
3. Repeat until there are V-1 edges.

Week 10

啥也没有！这一周是 UCB 的春假！

Week 11

7 月 15 日

最后两部分需要记笔记的内容：Trie 和 拓扑排序，前者是补充的最后一种数据结构，后者是图论的一点拓展和收尾

Tries

懒了，开抄！字典树(或者叫做检索树)是针对字符串(即由 ASCII 码构成)的检索数据结构

让我们首先考虑一下对我们当前的 HashMap 实现的潜在改进。

特殊情况 1：字符键映射

如果我们知道我们的键只是 ASCII 字符，我们可以放弃我们的通用 HashMap，而是使用一个数组，其中数组中的每个索引对应于特定的 ASCII 字符：

1
2
3
4
5
6
7
8
9
10
11
12
public class DataIndexedCharMap<V> {
    private V[] items;
    public DataIndexedCharMap(int R) {
        items = (V[]) new Object[R];
    }
    public void put(char c, V val) {
        items[c] = val;
    }
    public V get(char c) {
        return items[c];
    }
}

上面是一个可能的实现，用于接受字符键的地图。值 R 代表可能字符的数量（例如 ASCII 的 128）。我们不再需要存储可能会影响运行时的任何桶（以额外内存为代价）。我们知道我们的数据将均匀分布。

特殊情况 2：字符串键映射

假设我们知道我们的键总是字符串。我们可以使用一种称为 Trie 的特殊数据结构。这种数据结构将字符串的每个字母存储为树中的一个节点。它在获取单词、添加单词和一些特殊字符串操作方面具有出色的性能。

Trie Demo Trie

假设我们想要存储单词”sam”、”sad”、”sap”、”same”、”a”和”awls”。我们希望创建一个数据结构，使我们能够将这些单词添加进去，并清楚地表明我们的集合包含这些单词，而不包含这些单词的任何后缀或前缀。

There are a few key ideas for Tries:

  • Every node stores only one letter.
  • Nodes can be shared by multiple keys.

Consider a Trie with the words “sam” and “sad” already in it:

When we add the word “sap”, we can make use of the fact that we already have the prefix “sa” in the Trie:

Adding “same” follows a similar procedure. We have the prefix “sam” in the Trie, so we can use it to our advantage:

When adding “a”, our first instinct may be to add an edge between the root and the existing “a” in our Trie:

However, this way would be a bit misleading because we do not know if the “a” is the start of the word “ame”. Instead, we create an entirely new node

这已经看起来很不错了！我们可以清楚地看到我们在 Trie 中添加的单词。然而，有一个问题。我们应该只在 Trie 中有单词”sam”、”sad”、”sap”、”same”、”a”和”awls”。根据我们当前的结构，我们无法确定哪些前缀应该被视为在 Trie 中，哪些不应该。例如，我们希望前缀”sam”在 Trie 中，但我们不希望”awl”或”aw”被视为在 Trie 中。

为了解决这个问题，我们将把每个字符串的最后一个字符涂成蓝色，以示该字符结尾的单词

现在我们完成了！要搜索，我们将从根遍历我们的 Trie，并在下降时与我们正在搜索的字符串的每个字符进行比较。因此，只有两种情况我们找不到一个字符串；要么最终节点是白色的，要么我们掉出了树。

Examples:

  • contains("sam"): true, blue node
  • contains("sa"): false, white node
  • contains("a"): true, blue node
  • contains("saq"): false, fell off tree

Demo：here

Advantages of Tries. Tries have very fast lookup times, as we only ever look at as many characters as they are in the data we’re trying to retrieve. However, their chief advantage is the ability to efficiently support various operations not supported by other map/set implementations including:

  • longestPrefixOf
  • prefixMatches
  • spell checking

Reductions and Decomposition

Topological Sorts

拓扑排序，是图的顶点的一种排序，使得对于每条有向边 u→v，u 在排序中位于 v 之前

为什么叫这个名字？这可以从拓扑学的角度来理解：拖动图中的各个结点，使得它们排成一行，满足所有箭头都朝右，即得到了一种拓扑排序的可能

image-20240721230413781

相关算法实现如下：

How can we find a topological sort? Take a moment to think of existing graph algorithms you already know could be helpful in solving this problem.

Topological Sort Algorithm:

  • Perform a DFS traversal from every vertex in the graph, not clearing markings in between traversals.
  • Record DFS postorder along the way.
  • Topological ordering is the reverse of the postorder.

Why it works: Each vertex v gets added to the end of the postorder list only after considering all descendants of v. Thus, when any v is added to the postorder list, all its descendants are already on the list. Thus reversing this list gives a topological ordering.

Since we’re simply using DFS, the runtime of this is O(V+E) where V and E are the number of nodes and edges in the graph respectively.

DAGs

有向无环图，这是拓扑排序的适用范围，也是很多算法的受限制范围

Shortest Path Algorithm for DAGs

介绍了拓扑排序，那么它有什么用呢？

回忆之前学过的 Dijkstra 算法，当 DAGs 中存在负边权时，算法可能会遭遇失败！那么能否在 D 算法的大体框架之上做出一些修改，使得其能够规避掉负边权的影响？

先想想为什么负边权会导致算法失效——在负边权的作用下，有时候我们会”放松”某条边，但是放松后相应的某些顶点距离却并没有被更新，这是由于负边权在放松机制下产生了一种类似于”穿越”的效果。如果先将图进行拓扑排序，再按照排序后的顶点顺序进行 D 算法的思路，便可完美规避负边权的影响！

Longest Paths

在不能利用循环刷步数的前提下，如何求最长路径？(其实这个问题至今无解，即使是最佳的可行性算法也是指数级别的时间，根本无法应用)

考虑将问题范围缩小到 DAG，这便是我们能解决的范畴了。事实上，使用的方法很像小学以及初中的数学思考题：

  1. Form a new copy of the graph, called G’, with all edge weights negated (signs flipped).
  2. Run DAG shortest paths on G’ yielding result X
  3. Flip the signs of all values in X.distTo. X.edgeTo is already correct.

Reductions and Decomposition

说了这大半天才扯到本章的标题，这到底指的是什么意思呢？——

用 SPT-DAG 的方法来解决 LPT-DAG 问题，便是一种 reduction 的策略。

This process is known as reduction. Since DAG-SPT can be used to solve DAG-LPT, we say that “DAG-LPT reduces to DAG-SPT.”

它的定义如下：

if any subroutine for task Q can be used to solve P, we say P reduces to Q

Perhaps a better term for what we’ve been accomplishing earlier in the course is decomposition - breaking a complex task into smaller parts. Using abstraction to make problem solving easier. This is the heart of computer science.

Courses > CS61B
#Data Structure #Java
CS61B 笔记
http://example.com/2024/08/19/CS61B_Notes/
作者
思源南路世一劈
发布于
2024年8月19日
许可协议