数字的表示

CS61C-数字的表达

即Number Representation

这一节主要介绍了二进制、十六进制、十进制的相关知识与互相转换的方法，同时也介绍了几种计算机中表示数字的方法，从无符号数到正负整数，再到补码等知识，各自具有相应的优缺点与使用场景

三种进制

二进制

• 使用0b开头来表示，例如：

  • 0b1001
  • 0b1011

• 与十进制的转换：

  • 直接按照对应幂的次数相乘相加即可

  • 例如：将0b01101转化成十进制：

    

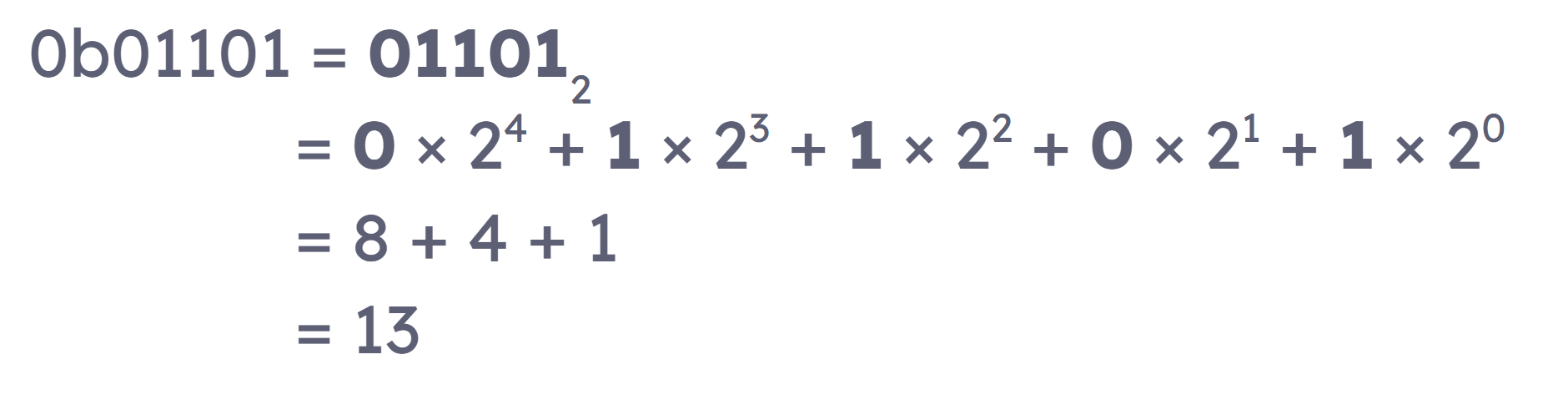
• 与十六进制的转换：

  • 先在左端补0，以使得总位数是4的倍数
  • 查表，翻译即可

  

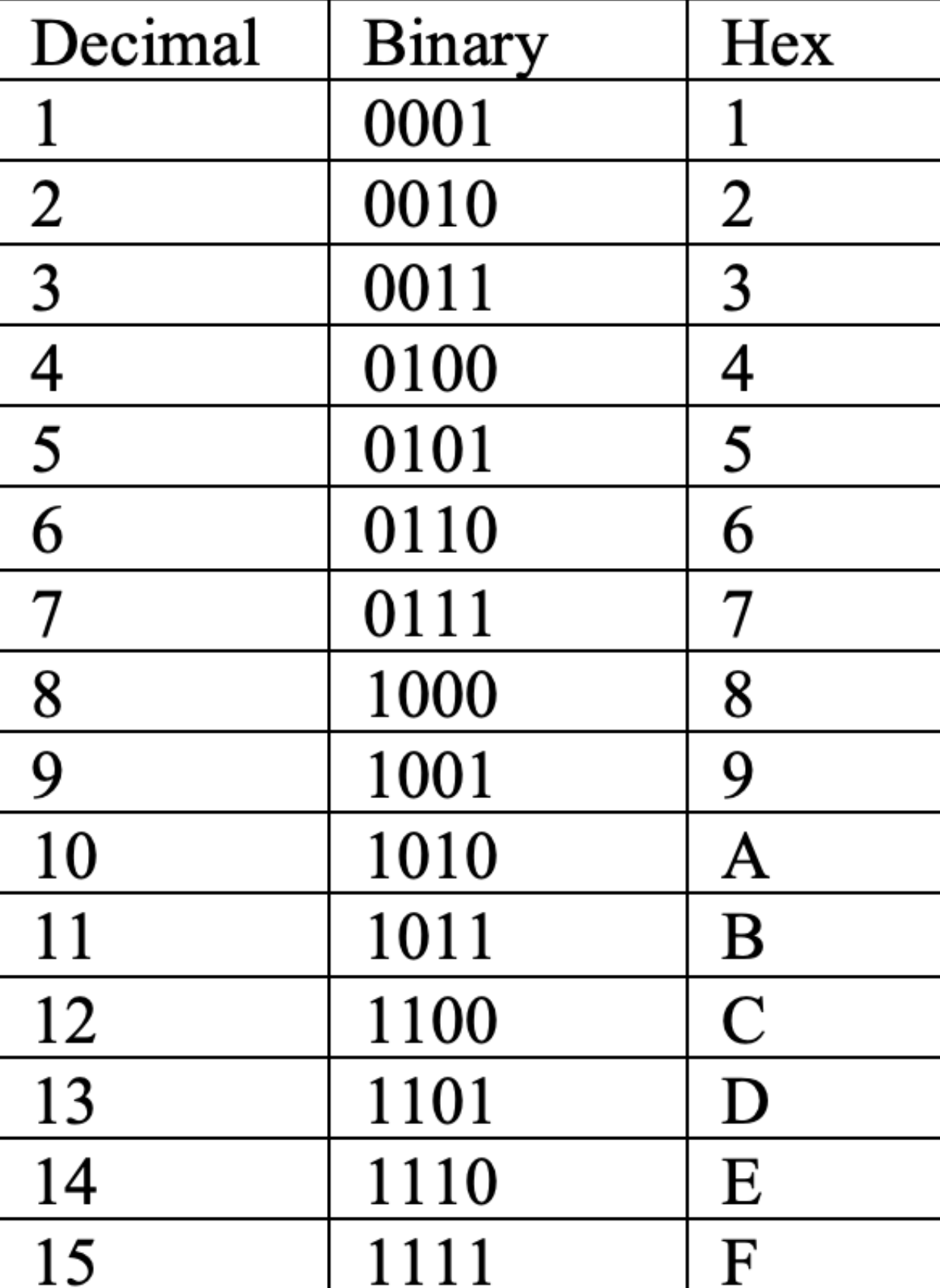
  • 例如：将0b1010011转化成十六进制：

  

• 特点：只需要用两种状态来表示，适合计算机使用

十六进制

• 使用0x开头来表示，超出10的数字用ABCDEF表示，例如：

  • 0x2B3C
  • 0xA1

• 与十进制的转换：和二进制类似，这里不在赘述

• 与二进制的转换：先查表，再删除多余的0即可

十进制

• 是日常生活中最常用的进制
• 与二进制、十六进制的转换：短除法，小学二年级就学过

数字的表示方法

无符号整数(Unsigned Integer)

直接使用二进制对应到十进制即可，例如0b00000000-0b11111111表示[0, 255]

n位的二进制数可以表示[0, 2^n-1]

用首位表示符号(Sign and Magnitude)

使用首位表示符号，其余位数表示绝对值，例如0b0000-0b1111表示[-7, 7]

n位的二进制数可以表示[1-2^n, 2^n-1]

优缺点：

• 优点
  • 便于理解
• 缺点
  • 有2个0
  • 算数运算不方便，不能直接在二进制数上操作
  • 在二进制数上+1可能会导致十进制数+1或者-1

现在已经不使用了，这里仅作介绍

二进制补码(Two’s Complement)

第一个位表示负，其余正，举例：

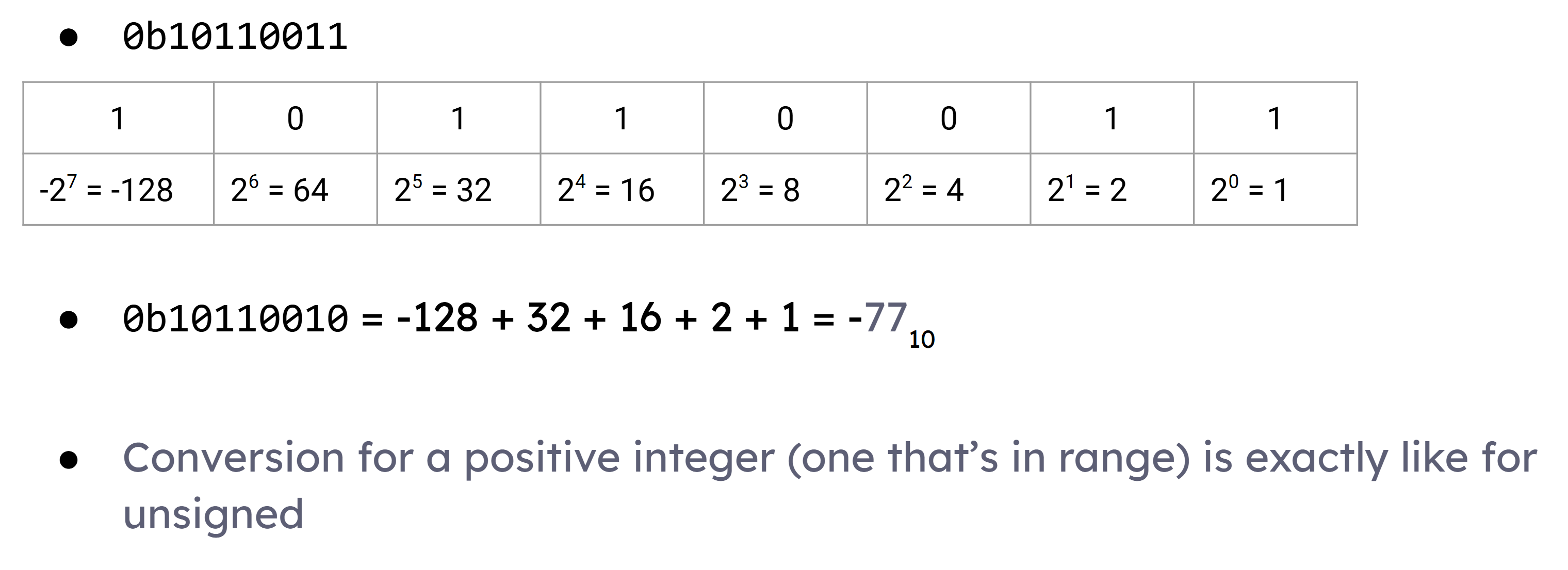
正数转换相同，下面解释如何转换负数：

• 二进制到十进制：
  • 翻转位数，0-1，1-0
  • 加1
  • 转换成十进制(这时候是正数)
  • 加上负号
• 十进制到二进制：
  • 去掉负号
  • 转换成二进制
  • 翻转位数，0-1，1-0
  • 加1

举例如下：

在这种情况下，整体表示数的范围就是一个环，但是最大的数过了之后就是最小的数，也即溢出(Overflow)

间隙表示(Bias Notation)

在无符号的基础上，直接加上一个bia即可，这个bia一般是负的

我们可以理解为将原本的表示范围向着数轴左端平移了一段距离得到的结果

当然这个平移的方向与距离视实际情况而定，一般来说是让0变成正中间

优缺点：

浮点数(Floating Point)

核心规则如下：

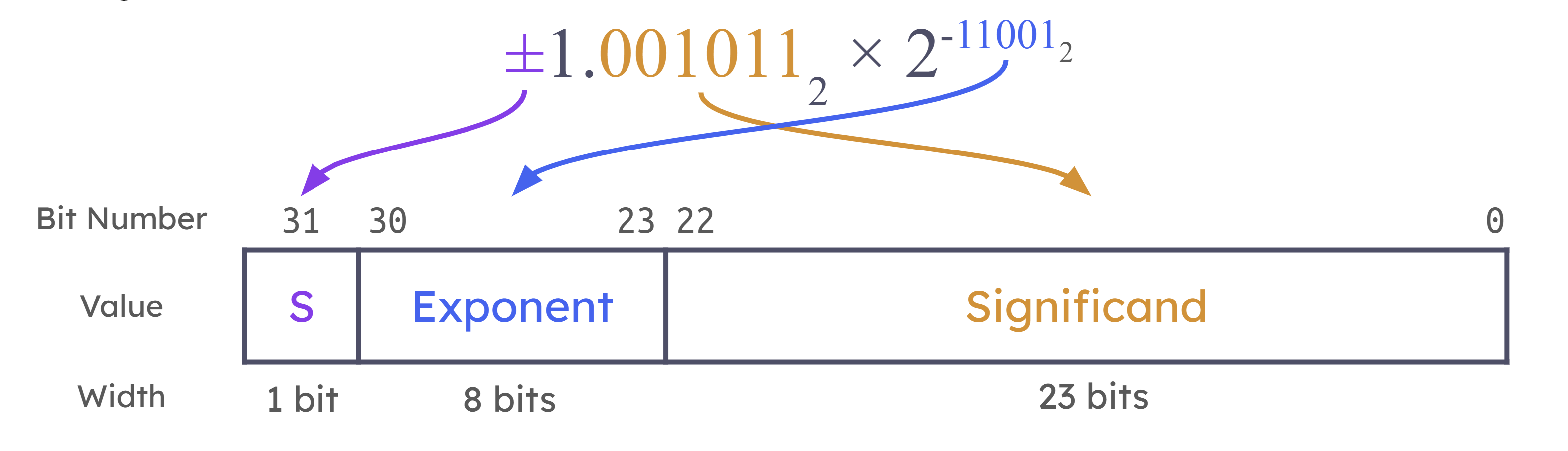
其中：

• Sign Bit：表示符号，0为+，1为-
• Exponent：表示指数，使用Bia Notation，其bia = -127
• Significand：表示底数的小数部分，使用二进制补码

整体计算规则如下：

一些特殊情况如下表所示：

其中NaN表示not a number